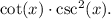Step-by-step explanation
Background
To solve the exercise, we need to recall two things: the common factor rule, and the cosecant's identity.
The common factor rule says that

The cosecant's identity says that
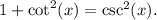
Solution of the exercise
Using the equations above, let's play a little with the expression of the exercise:

Answer