Solution:
Given:
![\begin{gathered} \text{The ratio of length to width of a rectangle=5:14} \\ \text{Perimeter}=152\operatorname{cm} \end{gathered}]()
Thus,
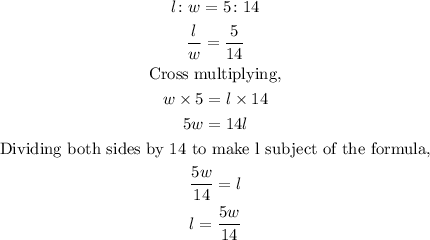
Also, recall that the perimeter of a rectangle is given by;
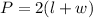
Hence,
![\begin{gathered} P=2(l+w) \\ 152=2((5w)/(14)+w) \\ (152)/(2)=(5w)/(14)+(w)/(1) \\ 76=(5w+14w)/(14) \\ 76=(19w)/(14) \\ \text{Cross multiplying,} \\ 76*14=19w \\ 1064=19w \\ \text{Dividing both sides by 19 to get the value of w,} \\ (1064)/(19)=w \\ w=56\operatorname{cm} \\ \\ \\ \text{Substituting the value of w gotten into;} \\ 5w=14l \\ 5*56=14l \\ 280=14l \\ \text{Dividing both sides by 14 to get the value of }l \\ (280)/(14)=l \\ l=20\operatorname{cm} \end{gathered}]()
Therefore, the length of the rectangle is 20cm.
The width of the rectangle is 56cm.
To get the area of the rectangle,
![\begin{gathered} \text{Area}=\text{length x width} \\ A=l* w \\ A=20*56 \\ A=1120\operatorname{cm} \end{gathered}]()
Therefore, the area of the rectangle is 1120 square centimeters.