We are asked if it is possible to write a polynomial of degree 4 with zeros at 5, 1-i, and 8i?
If we assume the polynomial has real coefficients, that is the polynomial can be expressed as:
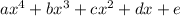
Where a, b, c, d,e are real numbers, it would be impossible to have a polynomial of degree four because the zeros at 1-i and 8i must have conjugates. This is because any polynomial with real coefficients and also has imaginary roots must have conjugates(and come in pairs).
Therefore, it would only be possible to have such a polynomial of degree 4 if the coefficients of the polynomial are complex.
ANSWER: No, if the coefficients of the polynomial of degree 4 are real, and yes if the coefficients are complex