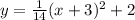Question

Write an equation of the parabola with the given characteristics

Answer 1

Given:

The focus of parabola is (-3,11/2).

The equation of directrix is y = -3/2.

Step-by-step explanation:

The general equation of parabola,

`y-k=(1)/(4p)(x-h)^2`

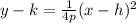
Then coordinates of focus is (h,k+p) and directrix equation is y = k - p.

On comparison with given focus and directrix equation,

`h=-3`
`k+p=(11)/(2)`
`k-p=-(3)/(2)`

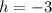
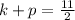
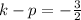
Add equation k + p = 11/2 and k - p = -3/2 to obtain the value of k.

`\begin{gathered} k+p+k-p=(11)/(2)-(3)/(2) \\ 2k=4 \\ k=2 \end{gathered}`

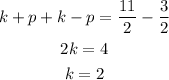
Determine the value of p.

`\begin{gathered} 2-p=-(3)/(2) \\ p=2+(3)/(2) \\ =(7)/(2) \end{gathered}`

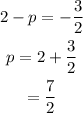
So value of h is -3, k is 2 and p is 7/2.

Determine the parabola equation for these h, p and k values.

`\begin{gathered} y-2=(1)/(4\cdot(7)/(2))(x-(-3))^2 \\ y=(1)/(14)(x+3)^2+2 \end{gathered}`

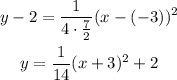
So equation of parabola is,

`y=(1)/(14)(x+3)^2+2`