Question

73733736635363363636464

Answer 1

According to the problem, the principal is $800, that's the investment.

For the first case (a), we have a simple interest rate of 4% and a time of 3 years. Let's use the simple interest formula

`A=P(1+rt)`

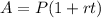
Then, let's replace the given values

`A=800(1+0.04\cdot3)=800(1+0.12)=800(1.12)=896`

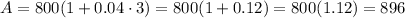
They will have $896.

On the other hand, for the second case (b), the compound interest is 3% compounded annually for 5 years. Let's use the compound interest formula

`A=P(1+(r)/(n))^(n\cdot t)`

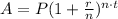
Where P = 800, r = 0.03, n = 1, and t = 5.

`\begin{gathered} A=800(1+(0.03)/(1))^(1\cdot5) \\ A=800(1.03)^5=927.42 \end{gathered}`

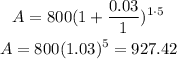
Hence, they will have $927.42 if the interest compounds annually.