Question

What is the expected value for the following probability distribution?

Answer 1

To calculate the expected value of our dataset, first we need to find the missing probability. The sum of the probabilities of all outcomes must add up to 1

`\sum P(X)=1`

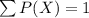
Therefore, 1 minus all the other probability values is going to be P(2).

`1-(0.04+0.05+0.2+0.1)=1-0.75=0.25`

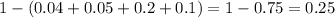
The expected value is given by the sum of every value of the dataset multiplied by its respective probability

`E[X\rbrack=\sum P(x_i)x_i`

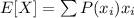
Using this formula in our problem, we have:

`\begin{gathered} E[X\rbrack=\sum_{i\mathop{=}1}^5P_i(x_i)x_i \\ =(0.4)*(0)+(0.05)*(1)+(0.25)*(2)+(0.2)*(3)+(0.1)*(4) \\ =0+0.05+0.5+0.6+0.4 \\ =1.55 \end{gathered}`

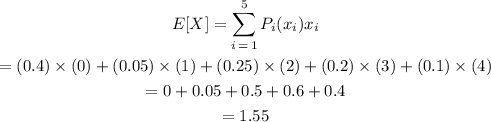
The expected value of this dataset is 1.55.