The problem already have a pathway to guide you to the answer, then let's follow it.
The first part, consists on writing the constrains and the objective function.
We have the following constrains:
- You need to run for at least 5 minutes;
- Row for at least 15 minutes;
- Your aerobics session should be no more than 30 minutes;
-You want to perform all three;
-The total workout is 60 minutes long.
Let's call the running time 'x', the rowing time 'y', and the time associated with the aerobics session 'z'.
Writing those constrains as inequalities goes like this
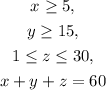
And the objective function(what we want to know), is the function that gives us the total amount of calories burnt in 60 minutes.
This function will be the sum of the products of each time by its respective rate.

The part B, consists in converting the into equations, and then use the substitution method to find four possible vertices.
We have four possibilites. Fixating 'z' on its minimum value and 'y' on its minimum, we get the following:
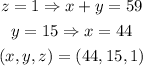
Fixating 'z' on its minimum value and 'x' on its minimum, we get the following:

Fixating 'z' on its maximum value and 'y' on its minimum, we get the following:
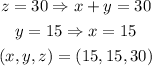
Fixating 'z' on its maximum value and 'x' on its minimum, we get the following:

On the last part, you just need to test the points we got on our objective function.
The function and the values:
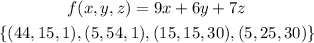
Calculating the function on each point:
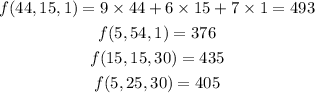
Comparing the results, we have the point (44, 15, 1 ) as the one that maximizes the function.