Question

List the potential rational zeros of the polynomial function. Do not find the zeros.

Answer 1

We can use the Rational Root Theorem to answer this question.

It says that, for a polynomial with integer coefficients, each rational solution:

`x=(p)/(q)`

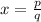
In lowest terms, can be found as:

- p is an integer factor of the constant term of the polynomial.

- q is an integer factor of the leading coefficient of the highest degree term of the polynomial.

That is, given the polynomial:

`6x^4+2x^3-3x^2+2`

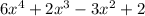
p must be a factor of 2 and q must be a factor of 6.

We also need to consider both positive and negative roots.

The factors of 2 are 1 and 2, so these are the options for p.

The factors of 6 are 1, 2, 3 and 6, so these are the options for q.

Now, we need to write every combination of p and q, considering both + and - signs:

`\pm(1)/(6),\pm(1)/(3),\pm(1)/(2),\pm(1)/(1),\pm(2)/(6),\pm(2)/(3),\pm(2)/(2),\pm(2)/(1)`

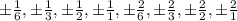
Now, we simplify:

`\pm(1)/(6),\pm(1)/(3),\pm(1)/(2),\pm1,\pm(1)/(3),\pm(2)/(3),\pm1,\pm2`

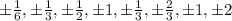
And we remove the repeating ones:

`\pm(1)/(6),\pm(1)/(3),\pm(1)/(2),\pm(2)/(3),\pm1,\pm2`

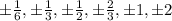
by comparison, we can see that it corresponds to the third alternative.