Question

Hello, I need some assistance with this homework question, please? This is for my precalculus homework. Q12

Answer 1

Given rational function:

`Q(x)\text{ = }(5x^2-17x-12)/(3x^2-10x-8)`

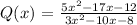
Vertical asymptote

To find the vertical asymptote, we set the denominator function to zero and solve for x

First, we factor the function.

`\begin{gathered} Q(x)\text{ =}(\left(5x+3\right)\left(x-4\right))/(\left(3x+2\right)\left(x-4\right)) \\ \end{gathered}`

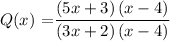
Since we can cancel (x-4) is present in the numerator and denominator, x= 4 is a hole

Setting the other factor in the denominator to zero:

`\begin{gathered} 3x\text{ + 2 = 0} \\ 3x\text{ = -2} \\ Divide\text{ both sides by 3} \\ \text{x = -}(2)/(3) \end{gathered}`

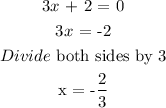
Hence, the vertical asymptote is x =-2/3

Horizontal asymptote

The first step is to compare the degrees of the numerator and denominator function. Since, the degrees are equal, we divide the leading co-efficients

Recall that the leading co-efficient is the coefficient of the term with the highest degree of the polynomial.

Hence, we have :

`\begin{gathered} y\text{ = }(5)/(3) \\ 5\text{ is the leading coeffient of the numerator function and 3 is the leading coefficient of the } \\ denominator\text{ function} \end{gathered}`

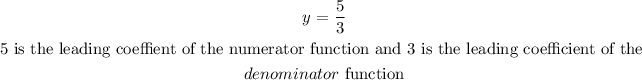
Hence, the horizontal asymptote is y = 5/3

Oblique asymptote

Oblique asymptotes occur when the degree of the denominator of a rational function is one less than the degree of the numerator.

Hence, there is no oblique asymptote