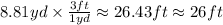Question

Schnortz has fenced in his 36 square yard circular garden. Next year, he plans to double the garden's area, but maintain its circular shape. To the nearest foot, how much more additional fencing will he need to enclose the garden next year?

Answer 1

Answer: 26ft

Step-by-step explanation

Given

• Has fenced in his 36 yr² circular garden.

,

• He plans to double the garden's area (36 yr² x 2), but maintain its circular shape.

The area of a circle (A) can be given with the following formula:

`A=\pi r^2`

where r represents the radius.

The edge of the area is covered with a fence, meaning that we have to find the perimeter given by the circumference (C ) of the garden to know how much fence we have. The circumference C can be calculated using the radius as follows:

`C=2\pi r`

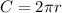
As we have the area that was fenced, we can calculate the radius using the formula for the area and then calculate the circumference with the radius.

0. Calculating the radius with the formula of the area.

`36=\pi r_1^2`

Simplifying:

`r_1^2=(36)/(\pi)`
`√(r_1^2)=\sqrt{(36)/(\pi)}`
`r_1=(6)/(√(\pi))`

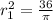
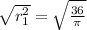
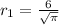
2. Replacing the radius to find the circumference:

`C_1=2\pi((6)/(√(\pi)))`

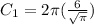
Simplifying:

`C_1\approx21.27yd`

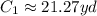
3. Next, we have to do the same but with the double of the area:

`36*2=\pi r_2^2`
`72=\pi r_2^2`
`r_2=\sqrt{(72)/(\pi)}`

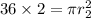
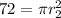
Now we have to replace it to find the circumference:

`C_2=2\pi(\sqrt{(72)/(\pi)})`
`C_2\approx30.08yd`

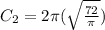
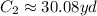
To calculate the additional fencing (Ca), we have to subtract the circumferences as follows:

`C_a=C_2-C_1`

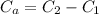
Replacing the values:

`C_a\approx30.08-21.27\approx8.81yd`

Finally, we have to convert them to foot, as we are asked in the problem:

`8.81yd*(3ft)/(1yd)\approx26.43ft\approx26ft`