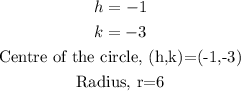Answer:
• Centre of the circle, (h,k)=(-1,-3)
,
• Radius = 6
Step-by-step explanation:
The standard form of the equation of a circle is:
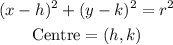
Given the circle below:
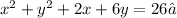
First, we reorder the terms.
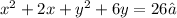
Next, we complete the square for the quadratics in x and y as shown below:
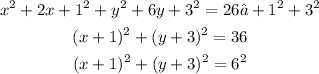
Comparing with the standard form given above: