Answer:
(a) magnitude: 9.96 m/s
Direction: 64.67°
(b) 158268.16 Joules
Step-by-step explanation:
Part (a)
We need to apply the conservation of momentum in each direction, so
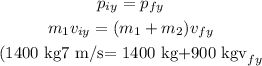
Solving for vfy, we get:
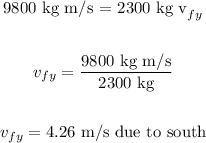
For the horizontal direction, we get:

Now, we can calculate the magnitude and direction of the final velocity as follows
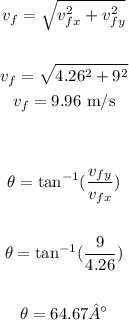
Part (b)
Then, the loss in kinetic energy can be calculated as:
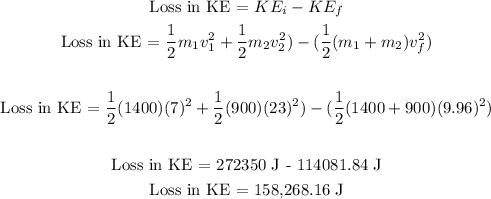
Therefore, the loss in kinetic energy was 158,268.16 Joules.