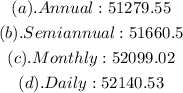Given:
There are given that the total amount is 34900 dollars
Step-by-step explanation:
According to the question:
We need to find the value of the investment.
So,
To find the value of investments, we need to use the compound interest formula:
So,
From the formula of compound interest:
(a): For annually:
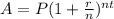
Then,
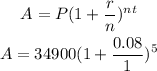
Then,
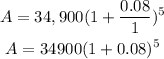
Then,

Now,
(b): For the semiannual:
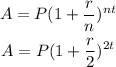
Then,
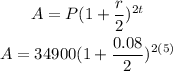
Then,
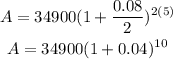
Then,
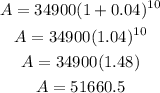
(c): For monthly:
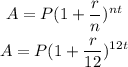
Then,
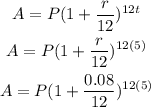
Then,
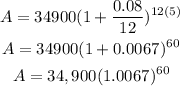
Then,
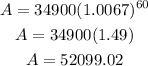
And,
(d): For daily:
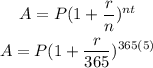
Then,
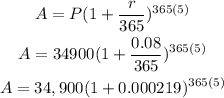
Then,

Final answer:
Hence, the all values is shown below: