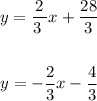Question

Find the center, vertices, foci, and asymptotes of the hyperbola.(y=4)? (x+8).-= 149Center: ODVertices: (01) and (-DFoci: CD and CDAsymptotes: y = and y = 0

Answer 1

we have the equation

`((y-4)^2)/(4)-((x+8)^2)/(9)=1`

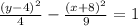
Part 1

Find out the center

The center is the ordered pair (-8,4)

Part 2

we have that

the transverse axis lies on the y-axis

a^2=4 ----------> a=2

b^2=9 --------> b=3

The coordinates of the vertices are

(-8,4+2) --------> (-8,6)

(-8,4-2) -------> (-8,2)

The vertices are (-8,6) and (-8,2)

Part 3

Find out the coordinates of Foci

Remember that

c^2=a^2+^2

c^2=4+9

c^2=13

c=√13

The coordinates of Foci are

(-8, 4+√13) and (-8,4-√13)

Part 4

Find out the equation of the asymptotes

The equation of te asymptotes is given bty

`y-k=\pm(a)/(b)(x-h)`

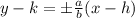
where

h=-8

k=4

a=2

b=3

substitute

therefore

the equations are

`\begin{gathered} y=(2)/(3)(x+8)+4=\frac{2}{3\text{ }}x+(16)/(3)+4=\frac{2}{3\text{ }}x+(28)/(3) \\ y=-(2)/(3)(x+8)+4=-(2)/(3)x-(16)/(3)+4=-(2)/(3)x-(4)/(3) \end{gathered}`

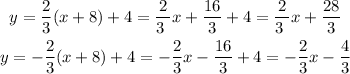
The asymptotes are

`\begin{gathered} y=\frac{2}{3\text{ }}x+(28)/(3) \\ \\ y=-(2)/(3)x-(4)/(3) \end{gathered}`