There is a proportional relation between the actual heights of 2 objects and their shadows at the same time
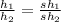
Since the shadow of the chimney is 32.5 m, then

Since the shadow of the pole is 2.72 m, then

Since the height of the pole is 2.4 m, then

Substitute them in the rule above
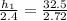
Use the cross-multiplication
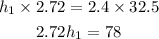
Divide both sides by 2.72
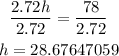
Round it to the nearest 2 decimal places
The height of the chimney is 28.68 m