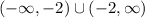Question

Finding the intercepts, asymptotes, domain and range

Added a photo!

Answer 1

See below

Explanation:

Vertical asymptotes are dashed lines formed where the denominator of a rational function is equal to 0. Hence, the given vertical asymptote of the function is x=-1.

Horizontal asymptotes are dashed lines where the output lies as the input increases. Hence, as x increases, y approaches -2, meaning that there's a horizontal asymptote at y=-2.

There is only one x-intercept which is -3 since the graph of the function intersects the x-axis only at that point.

There is only one y-intercept which is -6 since the graph of the function intersects the y-axis only at that point.

Given our vertical asymptote of x=-1, our domain is
`(-\infty,-1)\cup(-1,\infty)`

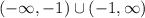
Given our horizontal asymptote of y=0, our range is
`(-\infty,-2)\cup(-2,\infty)`

Answer 2

Vertical -1
Hort: -2
X int: -3
Y-int: 6
Domain x does not equal -1
Range y does not equal -2

Please comment if problems!