Solution
To find the probability that exactly 2 don't grow?
This is a binomial probability question. The "success" here is that the seed doesn't grow, so
p = 1 - 0.95 = 0.05 q=0.95 n=8 (number of repetitions) r =2 (number of success)
where
P = success
q = failure
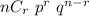
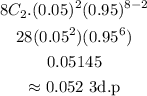
Therefore the probability that exactly 2 don't grow = 0.052 (3d.p)