To determine the focal length we will use the following formula:
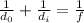
Where:

Now, we solve for "f". To do that we will add the fractions on the left side:
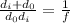
Now, we invert both sides:
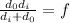
Substituting the values:
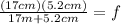
Solving the operations:
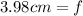
Therefore, the focal length is 3.98 cm.
The focal length and the radius are related by the following formula:
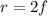
Where "r" is the radius. Substituting the value we get:

Solving the operations:
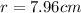
Therefore, the radius of curvature is 7.96 cm.