Question

F(x)= x² +5x-2 Find the vertex and the quadratic function in standard form

Answer 1

The given function is

`f(x)=x^2+5x-2`

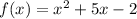
The vertex has two coordinates, h, and k. To find h we use the following formula.

`h=-(b)/(2a)`

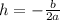
Where a = 1 and b = 5.

`h=-(5)/(2(1))=-(5)/(2)`

Then, we evaluate the function when x = -5/2 to find k.

`\begin{gathered} k=f(-(5)/(2))=(-(5)/(2))^2+5(-(5)/(2))-2 \\ k=(25)/(4)-(25)/(2)-2 \end{gathered}`

Let's find the least common factor between the denominators.

4 2 | 2

2 1 | 2

1

The least common factor would be 2*2 = 4, let's use it.

`\begin{gathered} k=(25-2\cdot25-4\cdot2)/(4) \\ k=(25-50-8)/(4) \\ k=-(33)/(4) \end{gathered}`

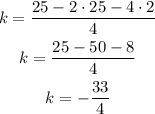
Once we know the value of h and k, we can deduct the vertex.

Therefore, the vertex is (-5/2, -33/4).

The standard form of a quadratic function is

`f(x)=a(x-h)^2+k`

In this case, a = 1, h = -5/2, and k = -33/4.

So, the standard form of f(x) is

`f(x)=(x+(5)/(2))^2-(33)/(4)`