Question

Find the arc-length of a circle with the given radius r and central angle 0. Give the answer in the given unit of measure, rounded to the nearesthundredthr = 20 km: 0 = 240°

Answer 1

The length of the arc of a circle whose radius is r and the angle of the arc is cita is

`L=r\theta`

Where cita is in the radian measure

Since r = 20 km

Since cita = 240 degrees

Change at first the measurement of the angle to radian by multiplying the degree measure by pi/180

`\begin{gathered} \theta=240*(\pi)/(180) \\ \theta=(4)/(3)\pi \end{gathered}`

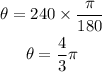
Substitute them in the rule above to find the length of the arc

`\begin{gathered} L=20*(4)/(3)\pi \\ L=83.7758041 \end{gathered}`

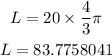
Round it to the nearest hundredth

L = 83.78 km

The length of the arc is 83.78 km