Question

Solve the following system of equations by graphing. Then determine wnether the system is consistent or inconsistent and whether theequations are dependent or independent. If the system is consistent, give the solution.-x + y = 53x + 3y = -27

Answer 1

Solving a System of Equation by Graphing

We have the system:

`\begin{cases}-x+y=5\ldots(1) \\ 3x+3y=-27\ldots(2)\end{cases}`

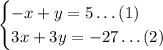
To find the solution by using graphs, we must graph each one of the lines in the same grid. If the lines actually meet at one point, that is the solution of the system. If the lines are equivalent (the same line) the system has infinitely many solutions. If the lines are parallel and don't ever meet, the system has no solution.

Let's start with the first equation:

-x + y = 5

Solving for y:

y = 5 + x

To draw a line, we only need two points, so we give x = 0 and then x = -5 and compute both values of y as follows:

For x = 0, y = 5 + 0 = 5

For x = -5, y = 5 - 5 = 0

The points are (0, 5) and (-5, 0). We join both points and draw the first line.

Now for the second equation:

3x + 3y = -27

Dividing by 3:

x + y = -9

Solving for y:

y = -x - 9

For x = 0, y = -9

For x = -9, y = 0

The points are (0, -9) and (-9, 0).

The graph with both lines is shown below:

The system is consistent and the solution is (-7, -2)

The equations of the lines in the slope-intercept form are:

y = x + 5

y = -x - 9

The equations are independent