Question

The question is in the Image and the Triangles I'm using. I already have answers for part C, But I'm not sure if they are correct. Topic: SSS Criterion for Similar Triangles

Answer 1

Part C

From the figure, each sides of both triangle are:

Triangle ABC

`\begin{gathered} AB\text{ = 3} \\ BC\text{ = 3} \\ AC\text{ = }\sqrt[]{AB^2+BC^2} \\ AC\text{ = }\sqrt[]{3^2+3^2} \\ AC\text{ = }\sqrt[]{9\text{ + 9}}\text{ = }\sqrt[]{18\text{ }}\text{ = 3}\sqrt[]{2} \end{gathered}`
`\begin{gathered} \text{From the triangle ABC} \\ \text{Opposite = 3} \\ \text{Adjacent = 3} \\ \text{Hypotenuse = 3}\sqrt[]{2} \\ \angle ABC\text{ = 90} \\ \angle ACB\text{ = 45} \\ \angle BAC\text{ = 45} \end{gathered}`

Next

For triangle DEF

DE = 6

EF = 6

DF = ?

`\begin{gathered} \text{Apply the pythagoras theorem} \\ DF\text{ = }\sqrt[]{DE^2+EF^2} \\ DF\text{ = }\sqrt[]{6^2+6^2} \\ DF\text{ = }\sqrt[]{36+36}\text{ = }\sqrt[]{72}\text{ = 6}\sqrt[]{2} \end{gathered}`
`\begin{gathered} \angle\text{EDF = 45} \\ \angle EFD\text{ = 45} \\ \angle DE\text{F = 90} \end{gathered}`

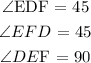
Part D

The two lengths have been increased by a scale factor of 2. The corresponding angle is the same.

Two triangles are similar if the angles are the same size or the corresponding sides are in the same ratio. Either of these conditions will prove two triangles are similar.

The two triangles are similar with SSS in the same proportion (side side side) All three pairs of corresponding sides are in the same proportion.

Triangle ABC is increased by a scale factor of 2 to triangle DEF.