Question

Multiply the rational expressions and express the product in simplest form. When typing your answer for the numerator and denominator be sure to type the term with the variable first.\frac{\left(x^2-x-6\right)}{\left(2x^2+x-6\right)}\cdot \frac{\left(2x^2+7x-15\right)}{\left(x^2-9\right)}The numerator is AnswerThe denominator is Answer

Answer 1

The given expression is

`((x^2-x-6))/((2x^2+x-6))\cdot((2x^2+7x-15))/((x^2-9))`

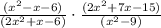
We have to factor all the expressions, one by one.

First expression.

`x^2-x-6`

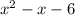
Let's use the quadratic formula to find the solutions.

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

Where a = 1, b = -1, and c = -6.

`\begin{gathered} x=\frac{-(-1)\pm\sqrt[]{(-1)^2-4(1)(-6)}}{2(1)}=\frac{1\pm\sqrt[]{1+24}}{2}=\frac{1\pm\sqrt[]{25}_{}}{2}=(1\pm5)/(2) \\ x_1=\frac{1+5_{}}{2}=(6)/(2)=3\to(x-3) \\ x_2=(1-5)/(2)=(-4)/(2)=-2\to(x+2) \end{gathered}`

So, the expression in factored form is (x+2)(x-3).

Second expression.

`2x^2+x-6`

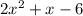
Where a = 2, b = 1, and c = -6. Let's repeat the process.

`\begin{gathered} x=\frac{-1\pm\sqrt[]{1^2-4(2)(-6)}}{2(2)}=\frac{-1\pm\sqrt[]{1+48}}{4}=\frac{-1\pm\sqrt[]{49}}{4}=(-1\pm7)/(4) \\ x_1=(-1+7)/(4)=(6)/(4)=(3)/(2)\to(2x-3) \\ x_2=\frac{-1-7_{}}{4}=-(8)/(4)=-2\to(x+2) \end{gathered}`

So, the expression in factored form is (2x-3)(x+2).

Third expression.

`2x^2+7x-15`

Where a = 2, b = 7, and c = -15.

`\begin{gathered} x=\frac{-7\pm\sqrt[]{7^2-4(2)(-15)}}{2(2)}=\frac{-7\pm\sqrt[]{49+120}}{4}=\frac{-7\pm\sqrt[]{169}}{4}=(-7\pm13)/(4) \\ x_1=(-7+13)/(4)=(6)/(4)=(3)/(2)\to(2x-3) \\ x_2=(-7-13)/(4)=(-20)/(4)=-5\to(x+5) \end{gathered}`

The expression in factored form is (2x-3)(x+5).

Fourth expression.

`x^2-9`

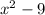
In this case, we have a difference between perfect squares, which can be solved using the following.

`a^2-b^2=(a+b)(a-b)`

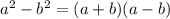
Where a^2 = x^2 and b^2 = 9.

`b^2=9\to b=\sqrt[]{9}\to b=3`

So, the expression in factored form is (x+3)(x-3).

Once we have all the factored forms, we simplify.

`((x+2)(x-3))/((2x-3)(x+2))\cdot((2x-3)(x+5))/((x+3)(x-3))=(x+5)/(x+3)`

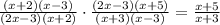
Therefore, the numerator is x+5, and the denominator is x+3.