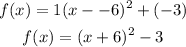Question

Write each function in vertex form, and identify its vertex. F(x)=x^2+12x+33

Answer 1

The vertex form of the quadratic function is

`f(x)=a(x-h)^2+k`

Where (h, k) are the coordinates of the vertex point

a is the coefficient of x^2

To find h use this rule

`h=-(b)/(2a)`

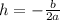
Where b is the coefficient of x

In our equation

The coefficient of x^2 is 1

a = 1

The coefficient of x is 12

b = 12

`h=-(12)/(2(1))=-(12)/(2)=-6`

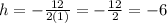
To find k substitute x by -6 in the equation

`k=(-6)^2+12(-6)+33=36-72+33=-3`

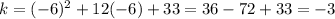
The vertex point is (-6, -3)

Let us substitute a, h, k in the vertex form above

`\begin{gathered} f(x)=1(x--6)^2+(-3) \\ f(x)=(x+6)^2-3 \end{gathered}`