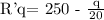Question A: Find the marginal cost as a function of q.
Given the following equation : C(q) = 90,000 + 80q
The marginal cost, C'(q0), will be:
C(q) = 90,000 + 80q
C'(q) = 0 + 80(1)
C'(q) = 80
Therefore, C'(q) = 80
Question B: Find the revenue function in terms of q.
The revenue function should be: (No. of microwaves sold) x (Price of microwave)
Where the equation for the price of the microwave is given at p = 250 - q/40.
Thus, the formula will be:

Therefore,
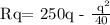
Question C: Find the marginal revenue function in terms of q.
![\text{R\operatorname{\lparen}q\operatorname{\rparen}=250q}\frac{(\text{q})^(2)}{40}]()
![\text{R'}\operatorname{\lparen}\text{q}\operatorname{\rparen}\text{=\lparen250\rparen\lparen1\rparen- }\frac{\text{q}^(2)}{40}\text{ = 250 - }\frac{\text{ q }}{20}]()
Therefore,