Question

Question 19 1 Level 4. Show all of your work to earn a 4. Directions: Write down the problem on a separate piece of paper and solve. Determine why the teacher marked Marc's answer incorrect. You will take a picture with your computers camera and attach it to this question. Problem: Marc writes - 470 . 2y-2.545 - 2-8 = –40xy and the teacher marked it wrong. Explain Marc's error and explain how to find the correct answer. (Reminder: you are going to write how your answer and her answer are different.) Upload Choose a File

Answer 1

Mark writes the following expression:

`-4x^3\ast2y^(-2)\ast5y^5\ast x^(-8)=-40x^5y^3`

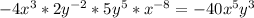
First, the problem deals with multiplication of terms with the same base and different exponents. In this case, we keep the base and add the exponents.

In this question:

Multiplying the numbers: -4*2*5 = -40

Terms with x:

`x^3\ast x^(-8)=x^(3-8)=x^5`

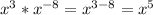
Terms with y:

`y^(-2)\ast y^5=y^(-2+5)=y^3`

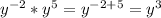
So the correct answer is:

`-40x^(-5)y^3`

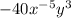
Marc's error happened in the addition of the exponents of x, as 3 - 8 = -5, not 5 like Marc founds.