Let A be the number of calories that contains candy bar A and let B be the number of calories that contains candy bar B. Then, given the information on the problem, we have the following system of equations:
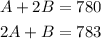
solving the first equation for A, we get:
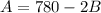
substituing this expression on the second equation, we get the following:
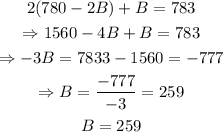
now that we have that B = 259, we can find the value of A using the first equation:
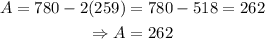
therefore, candy bar A contains 262 calories and candy bar B contains 259 calories