As you use the next formula o get the zeros in a quadratic function:
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
The possiblitity to have a imaginary zero is that ther part:
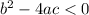
If that part is negative, then both zeros are imaginary because the square root of a negative number is a imaginary number and any real number add to an imaginary number is a complex number (a +bi, i is imaginary unit)
---------------------------------
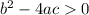
If that part is possitive both zeros are real numbers
Then, is not posible for a quadratic function to have one real zero and one imaginary zero. Because both zeros are real or both zeros are imaginary.