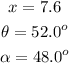Question

Round side lengths to the nearest tenth and round angle measures to the nearest degree. Include a labelled diagram of the triangle and show all your work.∡P=80°, r=8, p=10

Answer 1

Explanation:

Let us draw the triangle first.

Now, the law of cosines gives

`10^2=8^2+x^2-2\cdot8\cdot x\cos (80^o)`

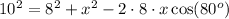
simplifying the above gives

`100=64+x^2-16x\cos (80^o)`

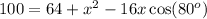
subtracting 64 from both sides gives

`100-64=x^2-16x\cos (80^o)`
`\Rightarrow36=x^2-16x\cos (80^o)`

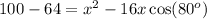
Rewriting the above in a more familiar form gives

`x^2-16\cos (80^o)x-36=0`

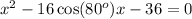
which is a quadratic equation.

Using the quadratic formula we solve for x and get

`x=\frac{16\cos (80^o)\pm\sqrt[]{(16\cos (80^o))^2-4(1)(-36)}}{2(1)}`

whose positive solution is

`\boxed{x=7.54791\ldots}`

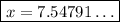
Next, we find the angle Θ.

To find Θ, we use the law of sines.

The law of sines in our case gives

`(10)/(\sin(80^o))=(8)/(\sin \theta)`

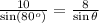
cross multipication gives

`10\sin \theta=8\sin (80^o)`

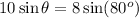
dividing both sides by 10 gives

`\sin \theta=(8\sin (80^o))/(10)`

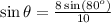
With the help of a calculator, we evaluate the right-hand side and get

`\sin \theta=0.787846`

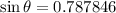
taking the inverse sine of both sides gives

`\begin{gathered} \boxed{\theta=51.984688^o\ldots^{}} \\ \end{gathered}`

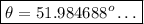
Last but not least, we find the value of α.

To find α, we use the fact that the sum of internal angles of a triangle must be 180°.

Therefore, we have

`\alpha+\theta+80^o=180^o`

putting in the value of Θ gives

`\alpha+51.984688^o+80^o=180^o`

simplifying and solving for α gives

`\boxed{\alpha=48.015^o}`

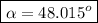
Hence, our angle and side length measures rounded to the nearest tenth are:

`\begin{gathered} x=7.6 \\ \theta=52.0^o \\ \alpha=48.0^o \end{gathered}`