Let x and y represent both numbers.
Given:
x = 1/4 * y
x + y = 15
Let's find the two numbers.
We have the system of equations:
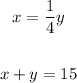
Plug in 1/4y for x in the second equation:
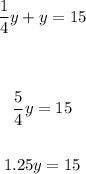
Divide both sides by 1.25:
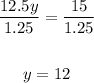
Now, to solve for x plug in 12 for y in either the first or second equation.
Let's take the first equation:
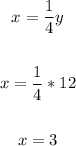
Therefore, the numbers are:
3, 12
ANSWER:
3, 12