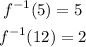ANSWER
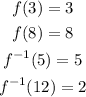
Step-by-step explanation
To identify the value of a function at a certain value of x, check the table for the value of f(x) that corresponds to the given value of x.
This means that:

To find the value of an inverse function of f(x), we have to note that the domain of a function is equal to the range of its inverse and the range of a function is equal to the domain of its inverse.
This means that the value of the inverse function of f is actually the value of x at the value of f(x).
This means that: