Question

Determine the number of lines symmetry for the figure. Select the angles of rotation, if any, that map the figure onto itself!

Answer 1

8 lines of symmetry

45°, 90°, 135, 180°

Explanation:

We know that a line of symmetry (line of symmetry or reflection symmetry) of a figure is a line that divides the figure into two congruent parts that are a mirror image of each other. therefore, we can determine the number of lines of symmetry like this:

Therefore, they are 8 lines of symmetry.

Now, the angles of rotation that make the figure remain unchanged would be the equivalent of each angle between each line of symmetry and its multiples. To calculate this angle, let's divide 360 by the number of petals that the flower has, that is, 8. Therefore:

`\begin{gathered} a=(360)/(8) \\ a=45\text{\degree} \end{gathered}`

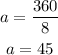
Therefore, the angles would be 45 ° and their multiples, that is, 90°, 135° and 180°