Question

Which of the following is a polynomial with roots negative square root of 3 , square root of 3 , and 2? (1 point)

Answer 1

Given that

The polynomial has the roots as

`-√(3),\text{ }√(3),\text{ and 2}`

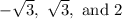
And we have to find the polynomial.

Explanation -

As there are 3 roots so the polynomial will have the highest degree 3.

Let the polynomial be y so according to the given roots it can be written as

`\begin{gathered} y=(x-√(3))*(x-(-√(3)))*(x-2) \\ \\ y=(x-√(3))(x+√(3))(x-2) \\ \\ Using\text{ the identity \lparen a+b\rparen\lparen a-b\rparen= a}^2-b^2 \\ so,\text{ } \\ y=(x^2-√(3)^2)(x-2) \\ \\ y=(x^2-3)(x-2) \\ \\ Using\text{ distributive property we have } \\ \\ y=x^3-2x^2-3x+6 \\ \\ y=x^3-2x^2-3x+6 \end{gathered}`

So the polynomial is y = x^3 - 2x^2 - 3x + 6

Final answer -

Hence the final answer is y = x^3 - 2x^2 - 3x + 6