Question

Patios plus sold an outdoor lighting set for $119.95. The markup on the set was $25.99. Find the markup percent on cost. Round to the nearest percent

Answer 1

- The question tells us that a lighting set is sold for $119.95. The markup was $25.99.

- The relationship between cost, markup, and selling price is given below:

`\begin{gathered} SP=CP+markup \\ \\ SP=CP+(n)/(100)* CP \\ \text{where,} \\ SP=\text{Selling price} \\ CP=\text{Cost price} \\ n=\text{markup percentage} \\ \\ \text{Thus, } \\ \text{markup}=(n)/(100)* CP \end{gathered}`

- SP = 119.95, CP = ?

- We need to find the cost price (CP) first

`\begin{gathered} SP=CP+\text{markup} \\ 119.95=CP+25.99 \\ CP=119.95-25.99 \\ \therefore CP=93.96 \end{gathered}`

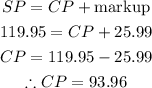
- Thus, we can find the markup percent as follows:

`\begin{gathered} \text{markup}=(n)/(100)* CP \\ \\ 25.99=(n)/(100)*93.96 \\ \\ \text{Make n the subject of the formula} \\ n=(25.99)/(93.96)*100 \\ \\ n=27.661\text{ \%}\approx28\text{ \%} \end{gathered}`

Final Answer

The markup percent is 28%