The equation representing the sum of the angles in triangle TVW is
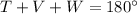 , which holds true for valid angle measurements within the triangle.
, which holds true for valid angle measurements within the triangle.
Yes, for both sets of angle measurements, the sum of the angles T, V, and W equals
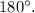 This consistency indicates that both sets of measurements represent valid angles within a triangle.
This consistency indicates that both sets of measurements represent valid angles within a triangle.
To create an equation representing this situation, you can use the fact that the sum of the interior angles of a triangle is always
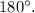
The equation representing the sum of the angles in the triangle TVW is:
![\[ T + V + W = 180^\circ \]](https://img.qammunity.org/2023/formulas/mathematics/college/xje42ta5p9tnrb63sphoa0bdfd34h3kqne.png)
This equation holds true for any valid measurements of the interior angles of a triangle. In this case, when
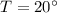 ,
,
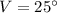 , and
, and
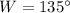 , their sum
, their sum
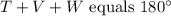 , satisfying the equation for a triangle's interior angles.
, satisfying the equation for a triangle's interior angles.