Question

Find the value of the test statistic z.The claim is that the proportion of peas with yellow pods is equal to 0.25 (or 25%). The sample statistics from one experiment include 430 peas with 126 of them having yellow pods.

Answer 1

You have to calculate the z-value or value of the test statistic z, for the proportion of yellow pods. The form of the z-statistic used to study the population proportion is:

`Z=\frac{\hat{p}-p}{\sqrt[]{(p(1-p))/(n)}}\approx N(0,1)`

The population proportion of the yellow pods is p=0.25.

From a sample of 430 peas, 126 of them had yellow pods, using this information you have to calculate the sample proportion p-hat (^p)

The sample proportion is equal to the quotient between the number of successful outcomes "x" (number of yellow pods) and the total number of outcomes "n" (number of peas sampled)

`\begin{gathered} \hat{p}=(x)/(n) \\ \hat{p}=(126)/(430) \\ \hat{p}=0.29 \end{gathered}`

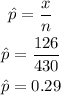
Once determined the sample proportion, you can calculate the z-value as follows:

`\begin{gathered} Z=\frac{0.29-0.25}{\sqrt[]{(0.25(1-0.25))/(430)}} \\ Z=\frac{0.04}{\sqrt[]{(0.25\cdot0.75)/(430)}} \\ Z=\frac{0.04}{\sqrt[]{(0.1875)/(430)}} \\ Z=1.915\approx1.92 \end{gathered}`

The value of the test statistic is 1.92.

*-*-*-*-*

The standard deviation of the distribution of the sample proportion:

To simplify the calculations you can calculate the standard deviation separately, the formula for this measure is the denominator of the formula of the Z-statistic:

`\sigma=\sqrt[]{(p(1-p))/(n)}`

Using p=0.25

`\begin{gathered} \sigma=\sqrt[]{(0.25(1-0.27))/(430)} \\ \sigma=\sqrt[]{(0.25\cdot0.75)/(430)} \\ \sigma=\sqrt[]{(0.1875)/(430)} \\ \sigma=\sqrt[]{(3)/(6880)} \\ \sigma=0.0208 \end{gathered}`

Then you can replace the result in the denominator of the formula to determine the Z-value:

`\begin{gathered} Z=\frac{\hat{p}-p}{\sqrt[]{(p(1-p))/(n)}} \\ Z=(0.29-0.25)/(0.0208) \\ Z=(0.04)/(0.0208)\approx1.92 \end{gathered}`