Select each answer choices that are correct for the slope of -2

Question

asked Oct 16, 2023 6.4k views

1 Answer

Cyril Cressent · Answer 1 · 2023-10-20T17:40:06+0000

The general equation of a circle is given as

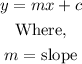
$\begin{gathered} y=mx+c \\ \text{Where,} \\ m=\text{slope} \end{gathered}$

The first equation is given as

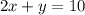
Making y the subject of the formula and then comparing coefficient

Subtract 2x from both sides

$\begin{gathered} 2x+y=10 \\ 2x-2x+y=10-2x \\ y=-2x+10 \\ \text{slope}=-2 \end{gathered}$

The second equation is given as

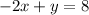
Add 2x to both sides and compare coefficients

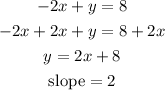
$\begin{gathered} -2x+y=8 \\ -2x+2x+y=8+2x \\ y=2x+8 \\ \text{slope}=2 \end{gathered}$

The third equation is given as

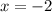
$\begin{gathered} x=-2 \\ \end{gathered}$

The equation above is a vertical line and hence, the slope is undefined

The fourth equation is given as

The equation above is a horizontal line and as such,the slope is zero

Considering the graph of the equation of the line attached below

Bringing out coordinates from the graph, we will have

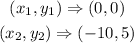
$\begin{gathered} (x_1,y_1)\Rightarrow(0,0) \\ (x_2,y_2)\Rightarrow(-10,5) \end{gathered}$

The slope of a line passing through points (x1,y1) and (x2,y2) is calculated using the formula below

By substituting the values, we will have

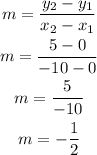
$\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ m=(5-0)/(-10-0) \\ m=(5)/(-10) \\ m=-(1)/(2) \end{gathered}$

Here, the slope is = -1/2

Considering the graph of the equation of the line attached below

Bringing out coordinates from the graph, we will have

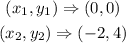
$\begin{gathered} (x_1,y_1)\Rightarrow(0,0) \\ (x_2,y_2)\Rightarrow(-2,4) \end{gathered}$

The slope of a line passing through points (x1,y1) and (x2,y2) is calculated using the formula below

By substituting the values, we will have

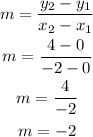
$\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ m=(4-0)/(-2-0) \\ m=(4)/(-2) \\ m=-2 \end{gathered}$

Here,the slope is = -2

Therefore,

The equation with a slope of -2 is 2x +y =10

while the graph with a slope of -2 is given below