Question

How can the square-root property be used to solve y2=6

Answer 1

Given the expression:

`y^2=6`

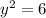
The first step to solve it using the square root property, is moving the coefficient on the right side of the equation to the left side, changing it's sign:

`\begin{gathered} y^2=6 \\ \Rightarrow y^2-6=0 \end{gathered}`

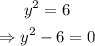
Now, remember the rule for conjugates:

`(a+b)(a-b)=a^2-b^2`

in this case we have the following:

`\begin{gathered} y^2=a^2 \\ \Rightarrow y=a \\ b^2=6 \\ \Rightarrow b=\sqrt[]{6} \end{gathered}`

therefore, we can factor the expression like this:

`\begin{gathered} y^2-6=0 \\ \Rightarrow(y-\sqrt[]{6})(y+\sqrt[]{6})=0 \end{gathered}`

Finally, we have that the only values that make true the expression are:

`\begin{gathered} y_1=\sqrt[]{6} \\ y_2=-\sqrt[]{6} \end{gathered}`