Question

The math teacher is buying math tools to use throughout thr year. he is planning on buying twice as many rulers as protractors. the number of calculators he is planning on buying is one quarter the number of protractors. if he buys 65 items how many of each does he buy?

Answer 1

Let's use the variable R to represent the number of rulers, the variable P for the number of protractors and the variable C for the number of calculators.

If the teacher will buy twice as many rulers as protractors, we have the equation:

`R=2P`

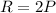
Then, if the number of calculators is one quarter of the number of protractors, we have:

`C=(P)/(4)`

The total number of itens is 65, so:

`R+P+C=65`

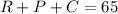
Using the values of R and C, we have:

`\begin{gathered} 2P+P+(P)/(4)=65 \\ (8P+4P+P)/(4)=(260)/(4) \\ 13P=260 \\ P=(260)/(13) \\ P=20 \\ \\ R=2P=2\cdot20=40 \\ C=(P)/(4)=(20)/(4)=5 \end{gathered}`

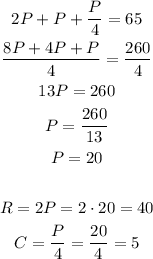
So the teacher bought 20 protractors, 40 rulers and 5 calculators.