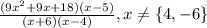Question

What is the product in simplest form? State any restrictions on the variable9X^2+9X+18)/(X+2) TIMES (x^2-3x-10)/(x^2+2x-24)

Answer 1

So, here we have the following expression:

`(9x^2+9x+18)/(x+2)\cdot(x^2-3x-10)/(x^2+2x-24)`

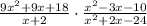
The first thing we need to notice before simplifying, is that the denominator can't be zero.

As you can see,

`\begin{gathered} x+2\\e0\to x\\e-2 \\ x^2+2x-24\\e0\to(x+6)(x-4)\\e0\to\begin{cases}x\\e-6 \\ x\\e4\end{cases} \end{gathered}`

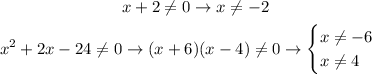
These are the restrictions on the given variable.

Now, we could start simplyfing factoring each term:

`\begin{gathered} (9x^2+9x+18)/(x+2)\cdot(x^2-3x-10)/(x^2+2x-24),x\\e\mleft\lbrace2,4,-6\mright\rbrace \\ \\ (9(x^2+x+2))/(x+2)\cdot((x-5)(x+2))/((x+6)(x-4)),x\\e\lbrace2,4,-6\rbrace \end{gathered}`

This is,

`9(x^2+x+2)\cdot((x-5))/((x+6)(x-4)),x\\e\lbrace4,-6\rbrace`

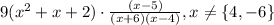
So, the answer is:

`(9(x^2+x+2)(x-5))/((x+6)(x-4)),x\\e\lbrace4,-6\rbrace`

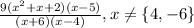
It could be also written as:

`((9x^2+9x+18)(x-5))/((x+6)(x-4)),x\\e\lbrace4,-6\rbrace`