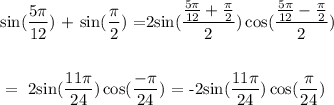Question

Would just like to make sure that my answer is correct.

Answer 1

`\text{ -2sin(}(11\pi)/(24))\cos ((\pi)/(24))`

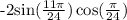
Step-by-step explanation:

Here, we want to simplify the given expression

The basic rule we will be using here is:

`\sin (A\text{ + B})\text{ = SinACosB + CosASinB}`

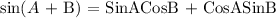
Thus, we have it that:

`\begin{gathered} \text{ sin(}(\pi)/(6)+(\pi)/(4))\text{ + sin(}(\pi)/(8)+(3\pi)/(8)) \\ \\ \sin ((5\pi)/(12))\text{ + sin(}(\pi)/(2)) \end{gathered}`

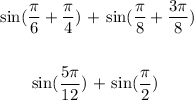
We use the sine addition formula as follows:

`\sin \text{ A + sin B = 2sin(}(A+B)/(2))\cos ((A-B)/(2))`

Now, we substitute the last expression into the given addition formula above:

`\begin{gathered} \text{ sin(}(5\pi)/(12))\text{ + sin(}(\pi)/(2))\text{ =2sin(}((5\pi)/(12)+(\pi)/(2))/(2))\cos (((5\pi)/(12)-(\pi)/(2))/(2)) \\ \\ =\text{ 2sin(}(11\pi)/(24))\cos ((-\pi)/(24))\text{ = -2sin(}(11\pi)/(24))\cos ((\pi)/(24)) \end{gathered}`