Explanation
We must find the product of complex numbers and write it in rectangular form i.e. like a+ib where a and b are real numbers. In order to do tthis we first need to write the values of the sine and cosine of 120° and 210°. For this purpose we can use a table displaying the values of the trigonometric functions for several angles. However, these tables usually display the values for angles between 0° and 90° like the following one:
However this table is still useful. 120° is an angle in the second quadrant which means that it has the same sine as an angle of the first quadrant that meets x=180°-120° and its cosine is the same but multiplied by -1. We have x=180°-120°=60° which means that:
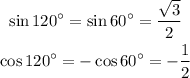
We can do something similar for 210°. It's in the third quadrant which means that both its sine and cosine are thoes of x=210°-180°=30° but multiplied by -1. Then we get:
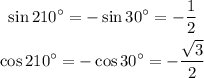
Now that we found the sine and cosine of both angles we can rewrite the product:
![\begin{gathered} \lbrack4(\cos210^(\circ)+i\sin210^(\circ))\rbrack\cdot\lbrack5(\cos(120^{\operatorname{\circ}})+\imaginaryI\sin(120^{\operatorname{\circ}}))\rbrack= \\ =\lbrack4(-(√(3))/(2)-i(1)/(2))\rbrack\cdot\lbrack5(-(1)/(2)+\mathrm{i}(√(3))/(2))\rbrack=\lbrack-2√(3)-2i\rbrack\cdot\lbrack-(5)/(2)+\mathrm{i}(5√(3))/(2)\rbrack \end{gathered}]()
Then we get:
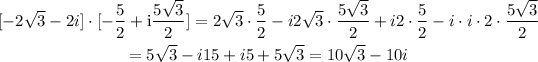
Answer
Then the answer is:
