We have a random discrete variable X, that takes values 1, 2 and 3.
As the probabilities of all the sample space is equal to 1.
So then we can define x in function of y:
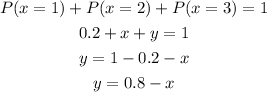
We can start by calculating the mean of X as:
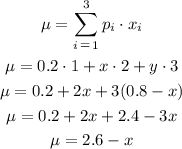
We can write the variance of X as:
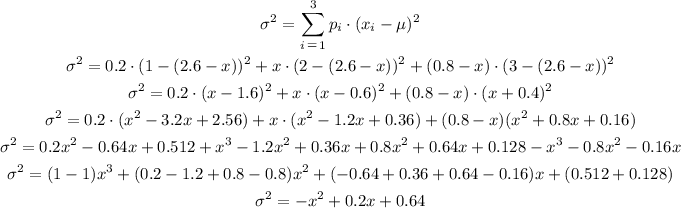
As the variance, σ², is equal to 0.29, then we can find the possible values for x as:
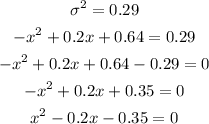
We can find the roots of this equation as:
![\begin{gathered} x=\frac{-(-0.2)\pm\sqrt[]{(-0.2)^2-4\cdot1\cdot(-0.35)}}{2\cdot1} \\ x=\frac{0.2\pm\sqrt[]{0.04+1.4}}{2} \\ x=\frac{0.2\pm\sqrt[]{1.44}}{2} \\ x=(0.2\pm1.2)/(2) \\ x_1=(0.2-1.2)/(2)=-(1)/(2)=-0.5 \\ x_2=(0.2+1.2)/(2)=(1.4)/(2)=0.7 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/hdxr60gr5i06mpciyvvcep7pzc9kvwptx5.png)
The value of x = -0.5, as it is a probability, has to have a value of between 0 and 1, is not valid.
Then, the only valid value for x is x = 0.7.
We then can calculate y as:
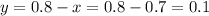
Answer: x = 0.7 and y = 0.1