The 25th term is 137
Step-by-step explanation:
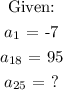
To get the 25th term, we need to find the common difference.
An arithmetic sequence is given as:
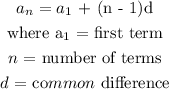
The formula for the 18th term will be used to find the common difference:
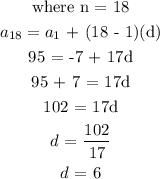
Now we can find the 25th term:
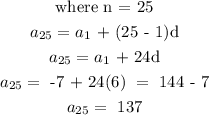
The 25th term is 137