Given the quadratic equation:
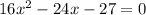
To find the solutions for the given equation you have to apply the quadratic formula:
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
Where
a is the coefficient of the quadratic term
b is the coefficient of the x-term
c is the constant of the equation
For this equation, a= 16, b= -24, and c= -27, replace the values into the formula:
![\begin{gathered} x=\frac{-(-24)\pm\sqrt[]{(-24)^2-4\cdot16\cdot(-27)}}{2\cdot16} \\ x=\frac{24\pm\sqrt[]{576+1728}}{32} \\ x=\frac{24\pm\sqrt[]{2304}}{32} \\ x=(24\pm48)/(32) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/l5kldd3nwwdn7x00z07c07d1kjdusjcge3.png)
Solve the addition and subtraction separately to determine both possible values of x:
-Addition:
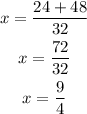
-Subtraction
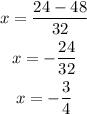
The solutions of the quadratic equation are x=9/4 and x=-3/4