A standard deck consists of 52 cards, and 4 of them are four. Our exercise is about probability without replacement.
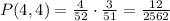
This is the fraction form of the probability, but we want the percentage form. To convert 12/2562 to the percentage form, we only need to multiply by 100:
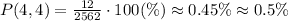
Comment 1: We round 0.45 to 0.5 because the second decimal place 5 is equal to 5 (this is a general rule).
Comment 2: The formula for P(4,4) I used is this:
![P(4,4)=\text{ (probability of choosing a four in the first drawn)}\cdot\text{(Probability of drawing a four in the second drawn)}]()
If we pick a four up in the first drawn, we have thus 51 cards, and just three fours to choose among them in the second drawn.