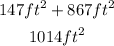Question

The figure shown is made up of a cone and a cylinder. The height of the cone is 5 ft and its diameter is 12 ft. The height of the cylinder is 20 ft.

Answer 1

Step-by-step explanation:

To figure out the lateral surface area of the cone, we will use the formula below

`A_(lateral)=\pi rl`

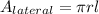
To figure out the slant height l, we will use the formula below

`\begin{gathered} l^2=5^2+6^2 \\ l^2=25+36 \\ l^2=61 \\ l=√(61) \end{gathered}`

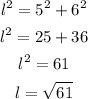
By substituting the values, we will have

`\begin{gathered} A_(lateral)=\pi rl \\ A_(lateral)=\pi*6*√(61) \\ A_(lateral)=147ft^2 \end{gathered}`

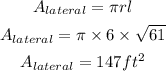
Hence,

The laterla surface area of the cone is

`147ft^2`

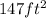
Part B:

To calculate the value of the are of the sides and bottom of the cylinder, we will use the formula below

`\begin{gathered} A_2=2\pi rh+\pi r^2 \\ where, \\ r=(12)/(2)ft=6ft \\ h=20ft \end{gathered}`

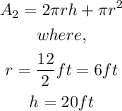
By substituting the values, we will have

`\begin{gathered} A_(2)=2\pi rh+\pi r^(2) \\ A_2=2\pi*6*20+\pi*6^2 \\ A_2=240\pi+36\pi \\ A_2=276\pi \\ A_2=867.08ft^2 \end{gathered}`

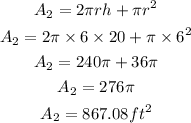
Hence,

The surface area of the sides and both if the cylinder is about

`867ft^2`

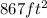
Part C:

The total surface area of the of the figure wil be

`\begin{gathered} 147ft^2+867ft^2 \\ 1014ft^2 \end{gathered}`