List all the possible subsets of Set H = { 4,3,6,5}

Question

asked Jul 6, 2023 37.0k views

1 Answer

← Prev Question Next Question →

Ask a Question

Cheri · Answer 1 · 2023-07-11T04:31:07+0000

Given Set H:

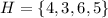
$H=\lbrace4,3,6,5\rbrace$

You can find the number of subsets the set has by using this formula:

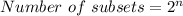
$Number\text{ }of\text{ }subsets=2^n$

Where "n" is the number of elements the set has.

In this case:

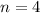
Then:

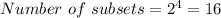
$Number\text{ }of\text{ }subsets=2^4=16$

By definition, given a set:

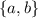
$\lbrace a,b\rbrace$

Its subsets are:

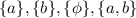
$\lbrace a\rbrace,\lbrace b\rbrace,\lbrace\phi\rbrace,\lbrace a,b\rbrace$

Therefore, in this case, you can determine that the possible subsets of the given set are:

$\lbrace4\rbrace,\lbrace3\rbrace,\lbrace6\rbrace,\lbrace5\rbrace,\lbrace4,3\rbrace,\lbrace4,6\rbrace,\lbrace4,5\rbrace,\lbrace3,6\rbrace,\lbrace3,5\rbrace,\lbrace6,5\rbrace,\lbrace4,3,6\rbrace,\lbrace3,6,5\rbrace,\lbrace4,6,5\rbrace,\lbrace4,3,5\rbrace,\lbrace4,3,6,5\rbrace,\lbrace\phi\rbrace$

Hence, the answer is:

$\lbrace4\rbrace,\lbrace3\rbrace,\lbrace6\rbrace,\lbrace5\rbrace,\lbrace4,3\rbrace,\lbrace4,6\rbrace,\lbrace4,5\rbrace,\lbrace3,6\rbrace,\lbrace3,5\rbrace,\lbrace6,5\rbrace,\lbrace4,3,6\rbrace,\lbrace3,6,5\rbrace,\lbrace4,6,5\rbrace,\lbrace4,3,5\rbrace,\lbrace4,3,6,5\rbrace,\lbrace\phi\rbrace$

List all the possible subsets of Set H = { 4,3,6,5}

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

Please log in or register to add a comment.

No related questions found

Categories

Other Questions