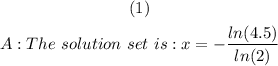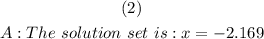Question

Hello, I need some assistance with this precalculus homework question, please?HW Q3

Answer 1

Step-by-step explanation:

Given:

We are given the following information;

`2^(-x)=4.5`

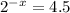
Required:

We are required to find the value of x (that is, the solution to this equation).

Step-by-step solution;

To do this we would re-write this equation by applying the law of exponents, which is as follows;

`\begin{gathered} If: \\ f(x)=g(x) \\ Then: \\ ln(f(x))=ln(g(x)) \end{gathered}`

With this, we will take the natural log of both sides of the equation;

`ln(2^(-x))=ln(4.5)`

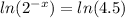
Next we, take the left side of the equation and apply the law of logs, as shown below;

`log_ba^x=xlog_ba`

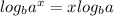
Therefore, we can refine the left side;

`ln(2^(-x))=-xln2`

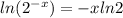
We can now re-write the entire equation as shown below;

`-xln2=ln4.5`

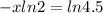
Divide both sides of the equation by ln(2);

`(-xln2)/(ln2)=(ln4.5)/(ln2)`
`-x=(ln(4.5))/(ln(2))`

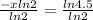
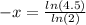
Multiply both sides of the equation by negative 1;

`x=-(ln(4.5))/(ln(2))`

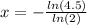
We now have the exact answer for x.

To solve for the value of x rounded to 3 decimal places;

`x=-(ln(4.5))/(ln(2))`

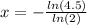
With the use of a calculator, we would now have;

`x=-(1.504077)/(0.693147)`
`x=-2.16992`

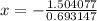
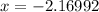
We can round this to 3 decimal places and we'll have;

`x=-2.169`

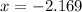
Therefore;

ANSWER:

`\begin{gathered} (1) \\ A:The\text{ }solution\text{ }set\text{ }is:x=-(ln(4.5))/(ln(2)) \end{gathered}`
`\begin{gathered} (2) \\ A:The\text{ }solution\text{ }set\text{ }is:x=-2.169 \end{gathered}`