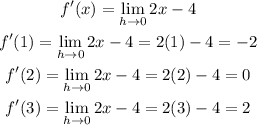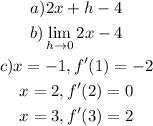
1) Considering that quadratic equation, we can find and simplify this expression that presents the limit of this function as h approaches 0.
a)
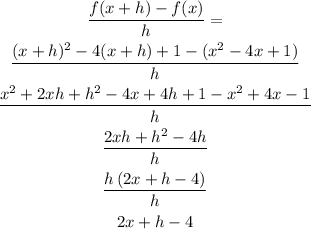
b) When h becomes very close to zero, we can find this:
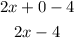
In other words, we find the limit of this function (or the first derivative) as h approaches 0.
c) Let's use this simplified expression to find the instantaneous rate of change at x=1,x=2, and x=3